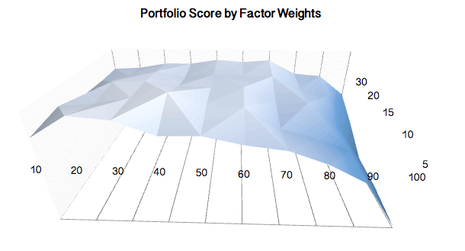
What can past returns tell us about future risk and returns?
Experiment writing trading and back-testing algorithms in Python (020218)
There is an ongoing debate among quants as to whether mean-reversion or momentum is dominant in predicting future prices. This seems to me as strange, as surely the data favours one or the other (or neither, in which case both are as useless as each other).
If I were to take a side, I would consider myself to be firmly in the "mean reversion" camp as I believe it is more likely to capture the extremes of investor emotion, buying when markets are depressed and selling when they get carried away. This makes sense to me, but it is difficult to find clean, fresh and unbiased data to prove or disprove this point of view.
Of course, I also accept that much of what we might call "momentum" also makes sense. A good example of this might be earnings announcements, which often take time to be reflected in the stock price. Other factors might include supply of capital, portfolio concentration and the endowment effect. Thinking back to the work by Ibbotson (et al) on liquidity premia, I was also interested in whether liquidity has any effect on these relationships.
If I were to take a side, I would consider myself to be firmly in the "mean reversion" camp as I believe it is more likely to capture the extremes of investor emotion, buying when markets are depressed and selling when they get carried away. This makes sense to me, but it is difficult to find clean, fresh and unbiased data to prove or disprove this point of view.
Of course, I also accept that much of what we might call "momentum" also makes sense. A good example of this might be earnings announcements, which often take time to be reflected in the stock price. Other factors might include supply of capital, portfolio concentration and the endowment effect. Thinking back to the work by Ibbotson (et al) on liquidity premia, I was also interested in whether liquidity has any effect on these relationships.
Process
To test the relationship between these investment styles, we first separated the market into high trade volume and low trade volume. Within each of these categories, qualifying stocks were ranked by decile on their performance from the last 5, 10, 15, 20 and 30 days; from each of these data points we then measured the forward week return. Data was recorded on a daily basis, rebalanced weekly.
This demands two sets of three-dimensional vectors. We chose the ten years to 31 January 2018 as our sample period.
Therefore we estimated the total number of data-points as follows:
To get around this we built an algorithm to do most of the heavy lifting for us.
We started by breaking the data down by liquidity (2) and performance decile (10), and then by Lookback Period (5). This reduces the total data load to around 2.08 million data points per trail, and provides us with a clear illustration of how a long-only portfolio might be expected to perform in each scenario (because of the ranking system, the results would look something like a momentum strategy for well-performing stock, and a mean-reversion strategy for the worst performing stock).
The next step was to write code to handle the performance of the remaining portfolio. I used Python to write an algorithm that called the security prices (US Equity market; c. 4,000 stocks) and filtered first by trade volume, then by decile. I then ordered the algorithm to make an equal-weight investment in each qualifying stock at the start of the week (Monday), before liquidating the entire portfolio before trade the following Monday, then doing it all over again (in the real world this would be very messy, however as we are ignoring taxes and brokerage costs it's the simplest way of extracting the information that we need).
At the end of the analysis period, the summary results were transferred to a simple Excel spreadsheet where I loaded a simple macro that allowed us to compare the results based and select "Qualifying Portfolios" based on client objectives (i.e., preference for high sharpe) and rules (i.e., at least 1% Alpha and Beta 0.2 below mean).
To test the relationship between these investment styles, we first separated the market into high trade volume and low trade volume. Within each of these categories, qualifying stocks were ranked by decile on their performance from the last 5, 10, 15, 20 and 30 days; from each of these data points we then measured the forward week return. Data was recorded on a daily basis, rebalanced weekly.
This demands two sets of three-dimensional vectors. We chose the ten years to 31 January 2018 as our sample period.
Therefore we estimated the total number of data-points as follows:
- Liquidity categories x 2
- Performance Decile x 10
- Lookback periods x 5
- Rank Record (p.a.) x 52
- Years Backtest x 10
To get around this we built an algorithm to do most of the heavy lifting for us.
We started by breaking the data down by liquidity (2) and performance decile (10), and then by Lookback Period (5). This reduces the total data load to around 2.08 million data points per trail, and provides us with a clear illustration of how a long-only portfolio might be expected to perform in each scenario (because of the ranking system, the results would look something like a momentum strategy for well-performing stock, and a mean-reversion strategy for the worst performing stock).
The next step was to write code to handle the performance of the remaining portfolio. I used Python to write an algorithm that called the security prices (US Equity market; c. 4,000 stocks) and filtered first by trade volume, then by decile. I then ordered the algorithm to make an equal-weight investment in each qualifying stock at the start of the week (Monday), before liquidating the entire portfolio before trade the following Monday, then doing it all over again (in the real world this would be very messy, however as we are ignoring taxes and brokerage costs it's the simplest way of extracting the information that we need).
At the end of the analysis period, the summary results were transferred to a simple Excel spreadsheet where I loaded a simple macro that allowed us to compare the results based and select "Qualifying Portfolios" based on client objectives (i.e., preference for high sharpe) and rules (i.e., at least 1% Alpha and Beta 0.2 below mean).
Results (Liquid Portfolios)
We start by looking at the results from our liquid portfolios. There were a number of results that I found surprising, and possibly useful in developing future risk management strategies. In particular, we find that mean reversion is by far the dominant factor in liquid portfolios, though it is more reliable in predicting future under-performance than out-performance. Moreover, those that have suffered the worst recent returns (worst 5%) are likely to continue under-performing. In fact, we found the highest Sharpe Ratios occurred in the 2nd and 3rd deciles (when ranking low to high). In contrast, the very best performers (best 1%) sustained the heaviest draw-down, worst return and lowest Sharpe.
We start by looking at the results from our liquid portfolios. There were a number of results that I found surprising, and possibly useful in developing future risk management strategies. In particular, we find that mean reversion is by far the dominant factor in liquid portfolios, though it is more reliable in predicting future under-performance than out-performance. Moreover, those that have suffered the worst recent returns (worst 5%) are likely to continue under-performing. In fact, we found the highest Sharpe Ratios occurred in the 2nd and 3rd deciles (when ranking low to high). In contrast, the very best performers (best 1%) sustained the heaviest draw-down, worst return and lowest Sharpe.
Are the results useful?
We have to be careful not to read too much into the results, especially given that our sample period includes the Global Financial Crisis and subsequent recovery. That aside, the bottom 50% of the market (decile 1:5) all outperformed the market over all look-back periods, with only the worst 1% recording significant underperformance.
We have to be careful not to read too much into the results, especially given that our sample period includes the Global Financial Crisis and subsequent recovery. That aside, the bottom 50% of the market (decile 1:5) all outperformed the market over all look-back periods, with only the worst 1% recording significant underperformance.
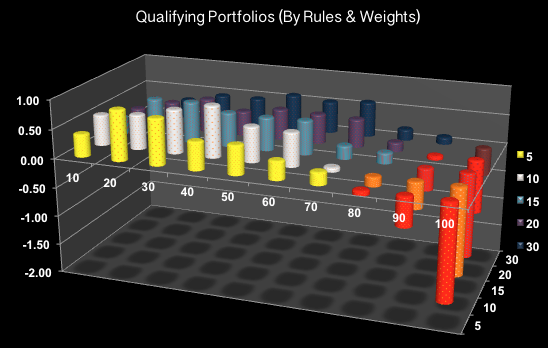 Example of Qualifying Portfolios: Factors: 3.5*SR -0.3*Beta + 1*Alpha; Rules: High liquidity + Sharpe>-1mu + Beta<+1mu + Alpha>-1mu
Example of Qualifying Portfolios: Factors: 3.5*SR -0.3*Beta + 1*Alpha; Rules: High liquidity + Sharpe>-1mu + Beta<+1mu + Alpha>-1mu
On the surface, this suggests there may be an opportunity for traders to enhance portfolio returns and/or reduce risk by concentrating their exposure on the most liquid but worst-performing stock.
By way of example, had we taken a levered equal-weighted exposure (150%) to the worst performing 30% of the market (ex very-worst 5%), while taking a short position (-100%) in the best performing 20% of the market, we would have seen the following changes to our investment results:
By way of example, had we taken a levered equal-weighted exposure (150%) to the worst performing 30% of the market (ex very-worst 5%), while taking a short position (-100%) in the best performing 20% of the market, we would have seen the following changes to our investment results:
- Return: +4.6% p.a.
- Beta: -0.34
- Sharpe Ratio: +0.18
- Max Drawdown: -16.72%
Results (Illiquid Portfolios)
Next we turn to the results from our illiquid portfolios (lowest 25% of market by trading value). Here the results become much more interesting .
As we would expect results were much more pronounced, with higher highs and lower lows across all measures. However, what was very surprising is we saw the worst performing stock continued to underperform, while the best performing stock continued to outperform by a significant margin, seemingly supporting a momentum-based approach.
Summary
These conflicting results are extremely interesting. Could it be that both mean-reversion and momentum styles work, but at different stages of a stock size or maturity?
If so, this might suggest that we use this information to help "weed out" stocks from our trading algorithm; for example, take long positions in the best performing illiquid and worst performing liquid, and take short positions in best performing liquid stocks (short position in worst performing illiquid might not be feasible, particularly when slippage is taken into consideration).
More research is needed, however, this provides a starting point to evaluating the relationship between past and future performance.
Model attributes:
Algorithm was built in Python and deployed via Quantopian using data from Quandl. 100 independent trials covering 2,000 stocks (4,000 / 2 liquidity filters) across 520 rebalancing periods. Approximately 208 million data points. Supplementary analysis (factor and rules based weightings) conducted through Excel.
Reference material:
Algorithmic Trading: Winning Strategies and Their Rationale, Chan, Ernest
Liquidity as an Investment Style, Ibbotson, R., Chen, Z, et al (https://www.cfapubs.org/doi/sum/10.2469/faj.v69.n3.4)
Kalman Filtering and Neural Networks, Haykin, Simon
GNU Octace (www.gnu.org)www.quantconnect.com
www.quantiacs.com
www.quantopian.com
www.quandl.com
Next we turn to the results from our illiquid portfolios (lowest 25% of market by trading value). Here the results become much more interesting .
As we would expect results were much more pronounced, with higher highs and lower lows across all measures. However, what was very surprising is we saw the worst performing stock continued to underperform, while the best performing stock continued to outperform by a significant margin, seemingly supporting a momentum-based approach.
Summary
These conflicting results are extremely interesting. Could it be that both mean-reversion and momentum styles work, but at different stages of a stock size or maturity?
If so, this might suggest that we use this information to help "weed out" stocks from our trading algorithm; for example, take long positions in the best performing illiquid and worst performing liquid, and take short positions in best performing liquid stocks (short position in worst performing illiquid might not be feasible, particularly when slippage is taken into consideration).
More research is needed, however, this provides a starting point to evaluating the relationship between past and future performance.
Model attributes:
Algorithm was built in Python and deployed via Quantopian using data from Quandl. 100 independent trials covering 2,000 stocks (4,000 / 2 liquidity filters) across 520 rebalancing periods. Approximately 208 million data points. Supplementary analysis (factor and rules based weightings) conducted through Excel.
Reference material:
Algorithmic Trading: Winning Strategies and Their Rationale, Chan, Ernest
Liquidity as an Investment Style, Ibbotson, R., Chen, Z, et al (https://www.cfapubs.org/doi/sum/10.2469/faj.v69.n3.4)
Kalman Filtering and Neural Networks, Haykin, Simon
GNU Octace (www.gnu.org)www.quantconnect.com
www.quantiacs.com
www.quantopian.com
www.quandl.com